Dijkstra’s Algorithm:

Article Goal

Explain in the most straightforward way how Dijkstra’s Algorithm works (With cool diagrams!). This is my first time writing and I figured this would be a fun way to get started!

Introduction to Dijkstra’s Algorithm

Every time you ask Google Maps for directions, book the cheapest flight, or even browse the internet, you’re benefiting from Dijkstra’s algorithm working behind the scenes. This elegant algorithm from the 1950s solves one of humanity’s most fundamental problems: finding the most efficient path between two points.

What makes Dijkstra’s algorithm so powerful isn’t just its mathematical elegance, it’s its versatility. Beyond navigation, it optimizes network routing (ensuring your Netflix stream takes the fastest path through the internet), powers social media friend suggestions (finding the shortest connection between people), and even helps in robotics, game AI, and supply chain logistics.

The algorithm is incredible IMO largely because of its simplicity, in the next sections we’ll dive into how it actually works.

Algorithm

1. Initialization
   • Set the distance to the origin node, $d[\text{origin}] = 0$.
   • Set the distance to all other nodes, $d[v] = \infty$ for $v \neq \text{origin}$.
   • Mark all nodes as unvisited.
   • Set the parent of each node to None.
2. Select Node
   • While there are unvisited nodes:
     • Pick the unvisited node $u$ with the smallest known distance $d[u]$.
3. Update Neighbors
   • For each neighbor $v$ of $u$:
     • Calculate the tentative distance: $d_{\text{tentative}} = d[u] + w(u, v)$, where $w(u, v)$ is the edge weight.
     • If $d_{\text{tentative}} < d[v]$:
       • Update $d[v] = d_{\text{tentative}}$.
       • Set the parent of $v$ to $u$.
4. Mark as Visited
   • Mark $u$ as visited (do not revisit).
5. Repeat
   • Repeat steps 2–4 until the destination node is visited or all reachable nodes have been visited.

The shortest path is then found by tracing the arrows from the goal vertex back to the source vertex.

Complexity

Time: $O((\vert V \vert + \vert E \vert) \log \vert V \vert)$ using a binary heap
Space: $O(\vert V \vert)$

Algorithm Requirements

Non-negative edge weights

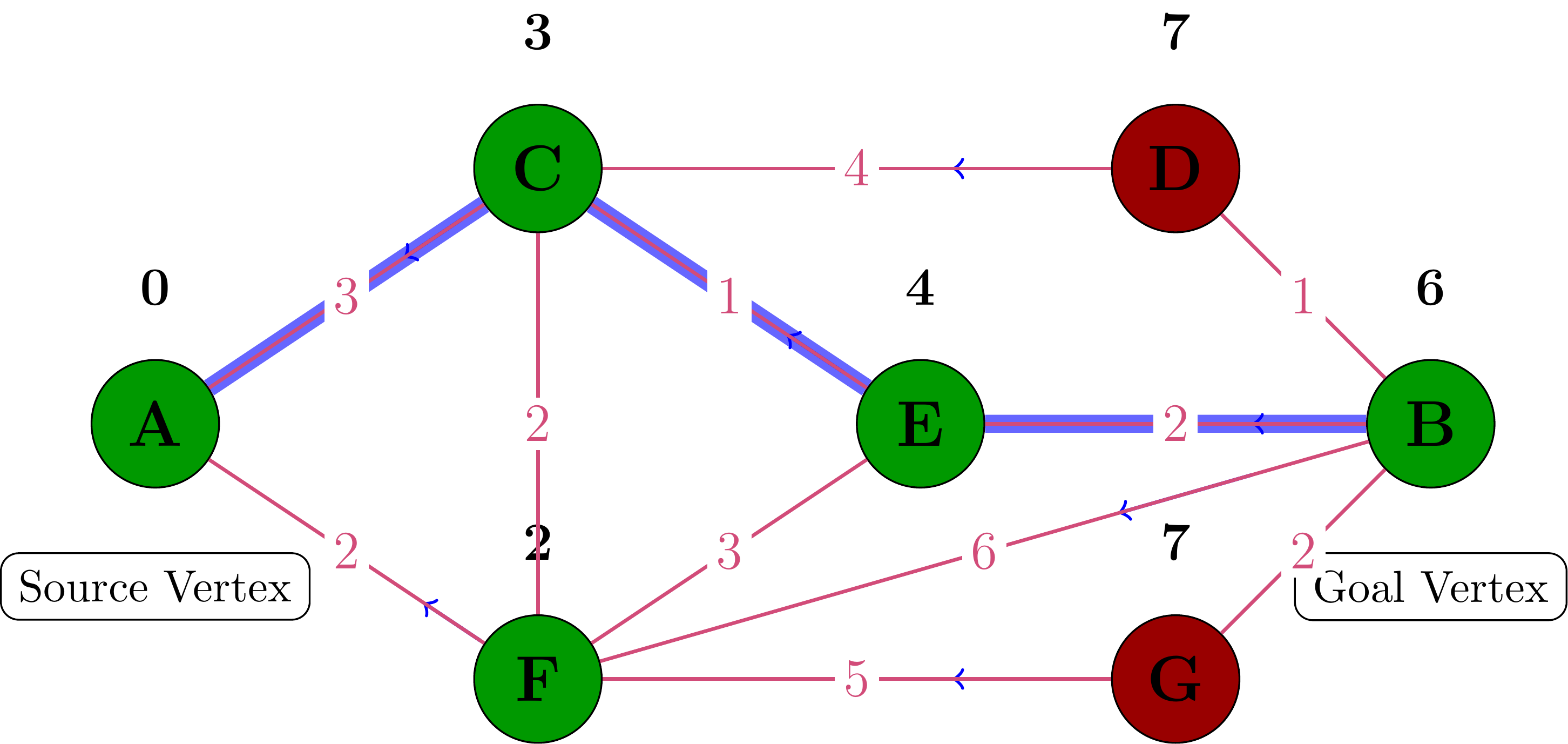
Simple Example

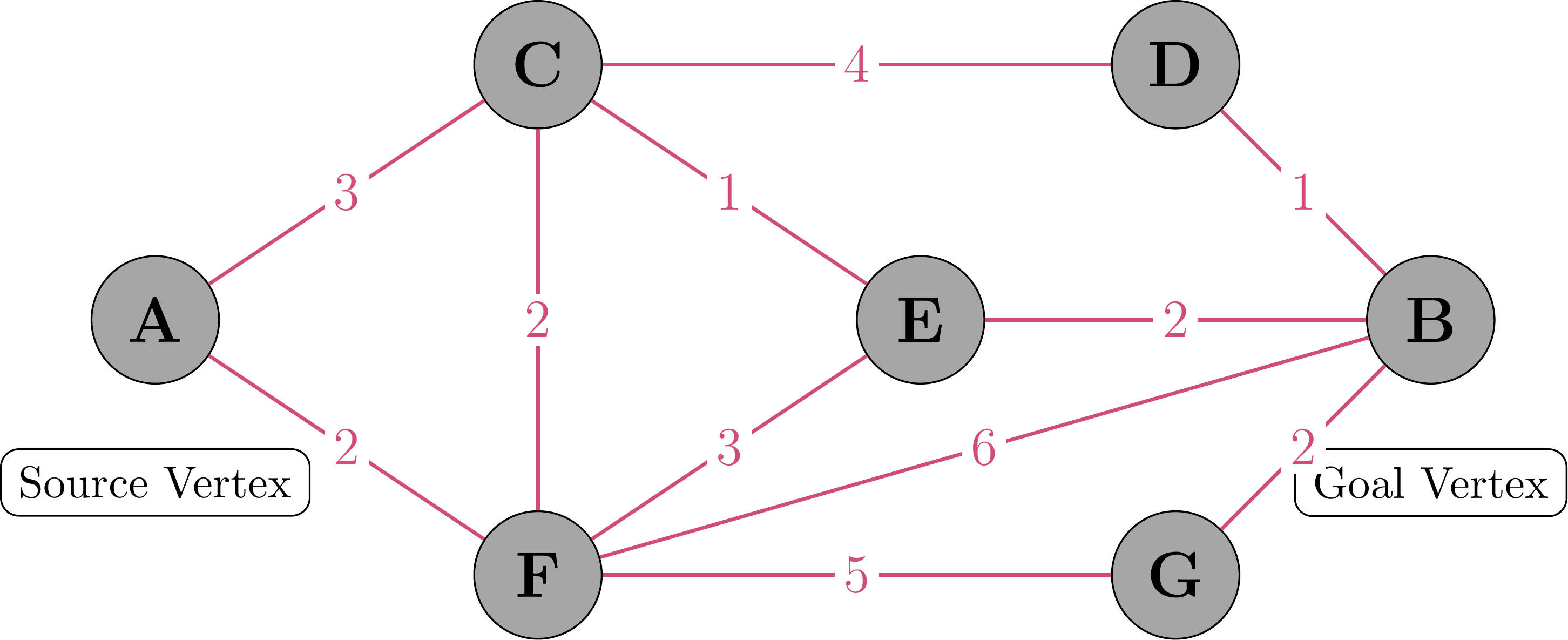
This graph shows a network of vertices connected by weighted edges. The goal is to find the shortest path from vertex A (source) to vertex B (goal) using Dijkstra’s algorithm.

Algorithm Initialization

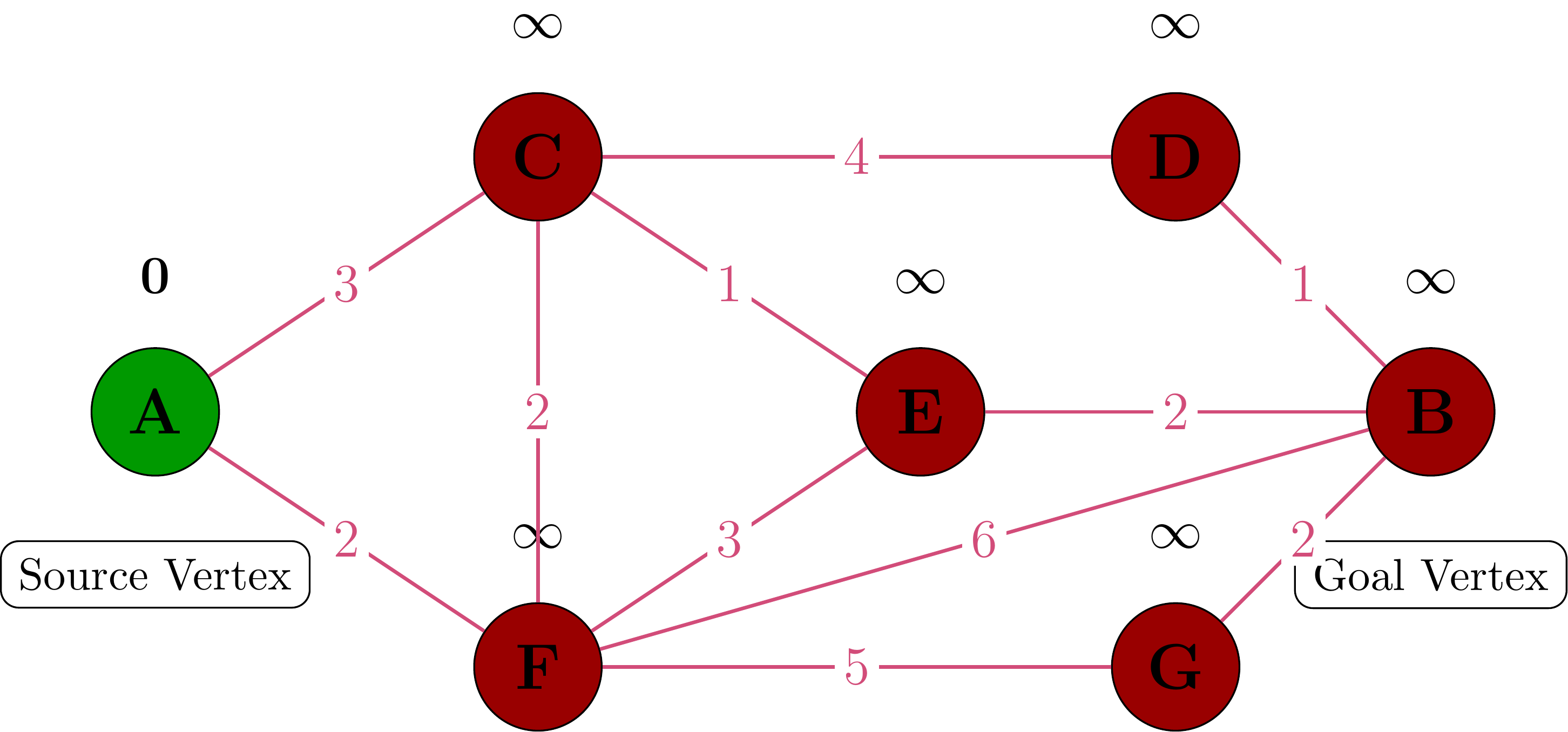
Processing Source Vertex A

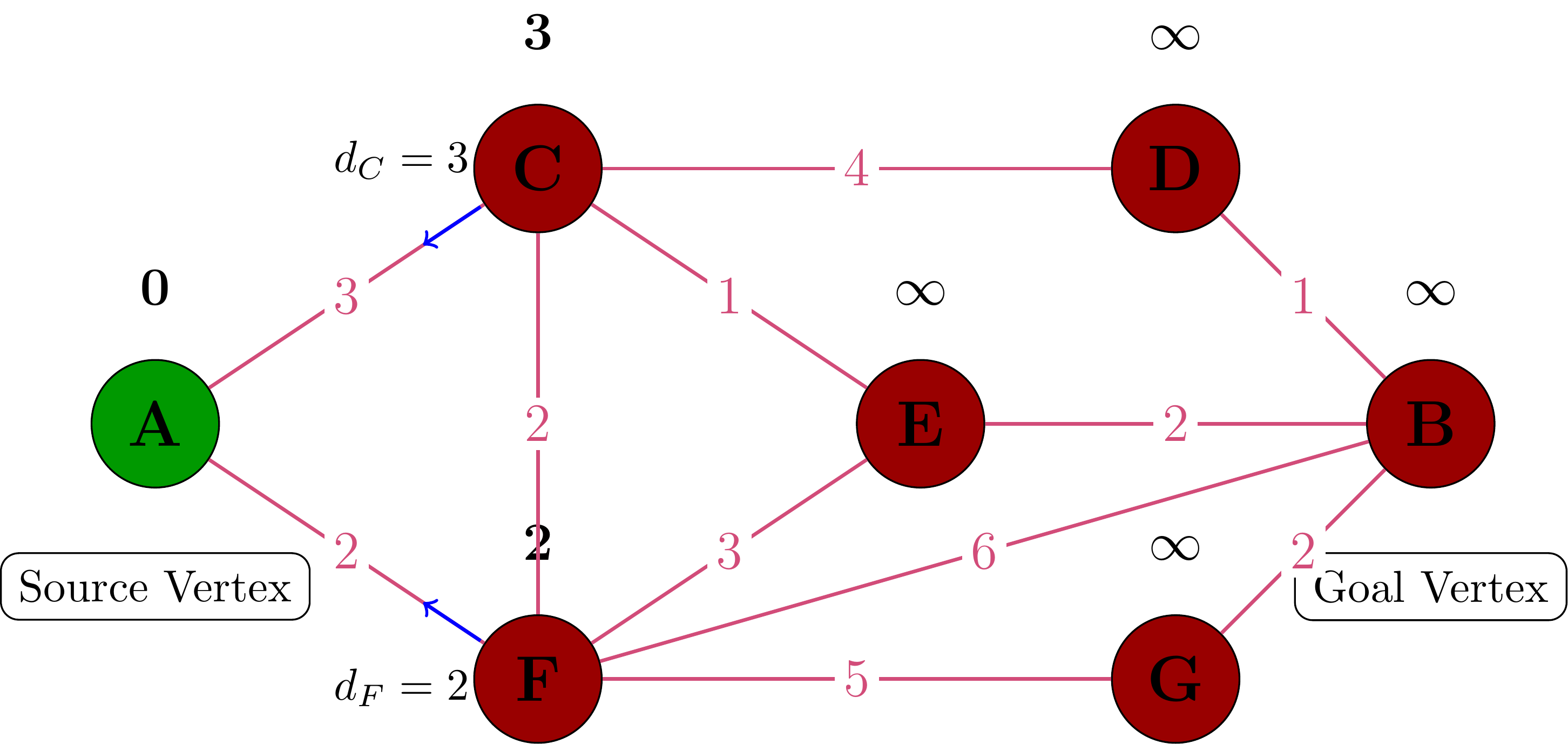
Processing Vertex F

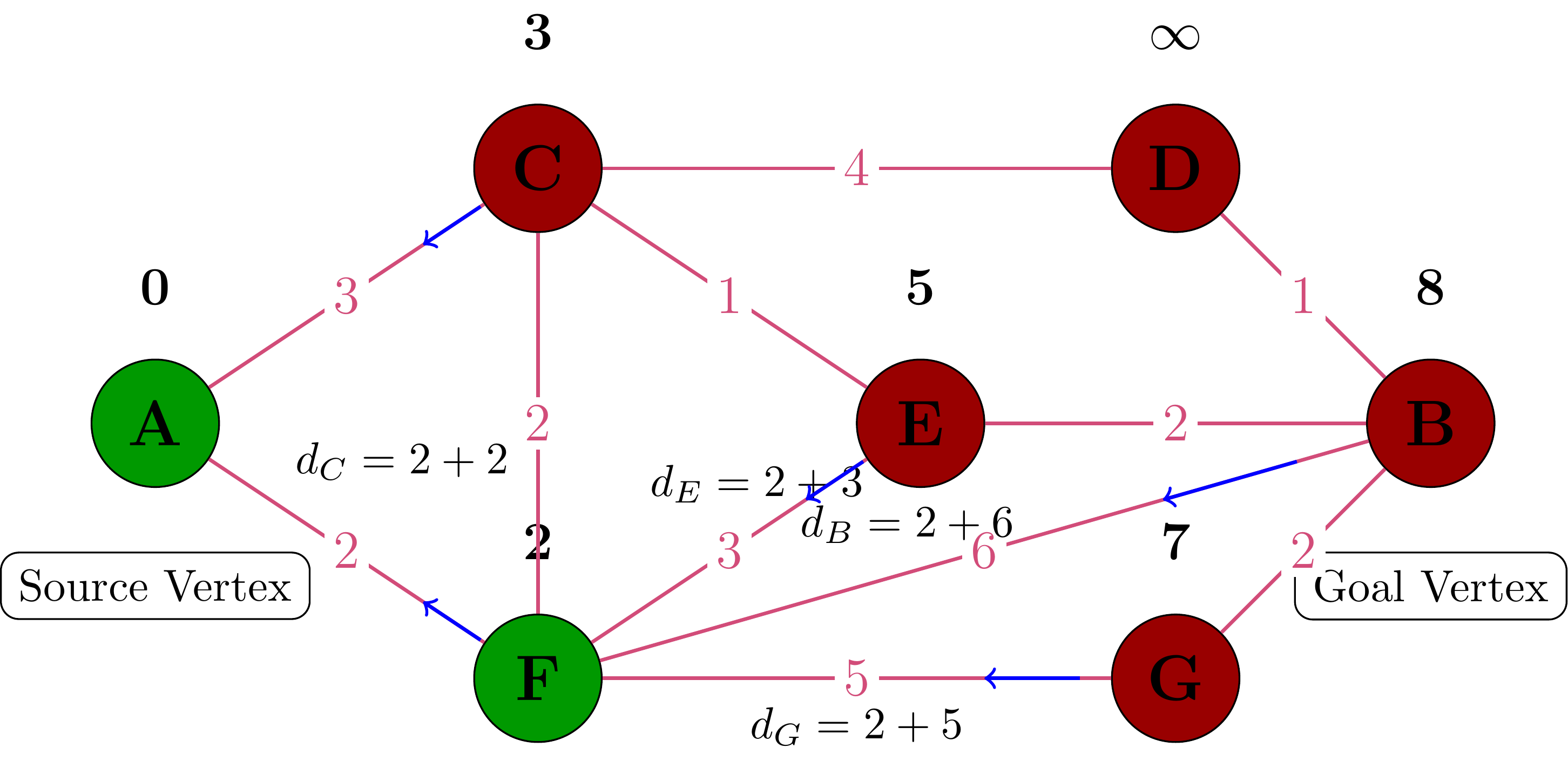
Processing Vertex C

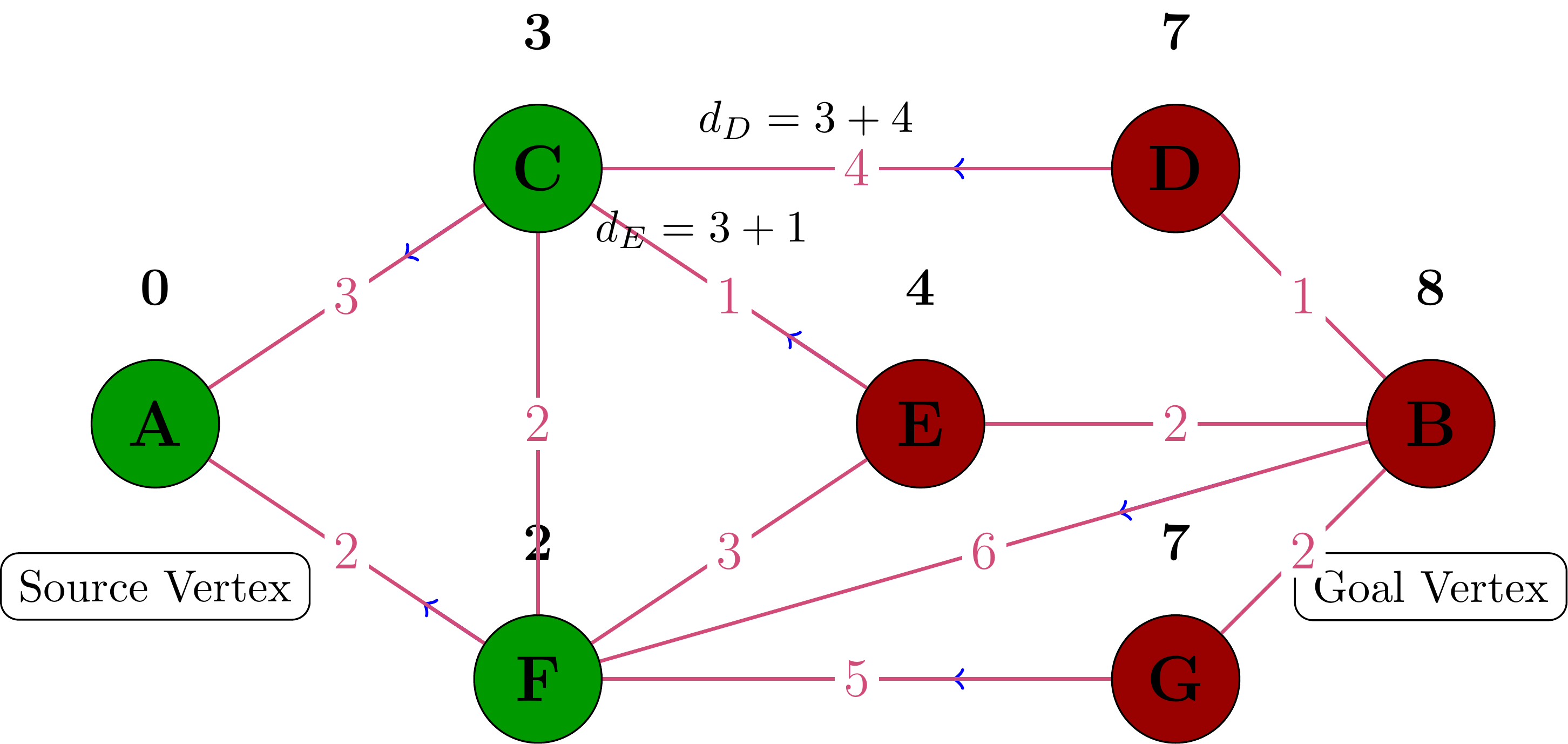
Processing Vertex E

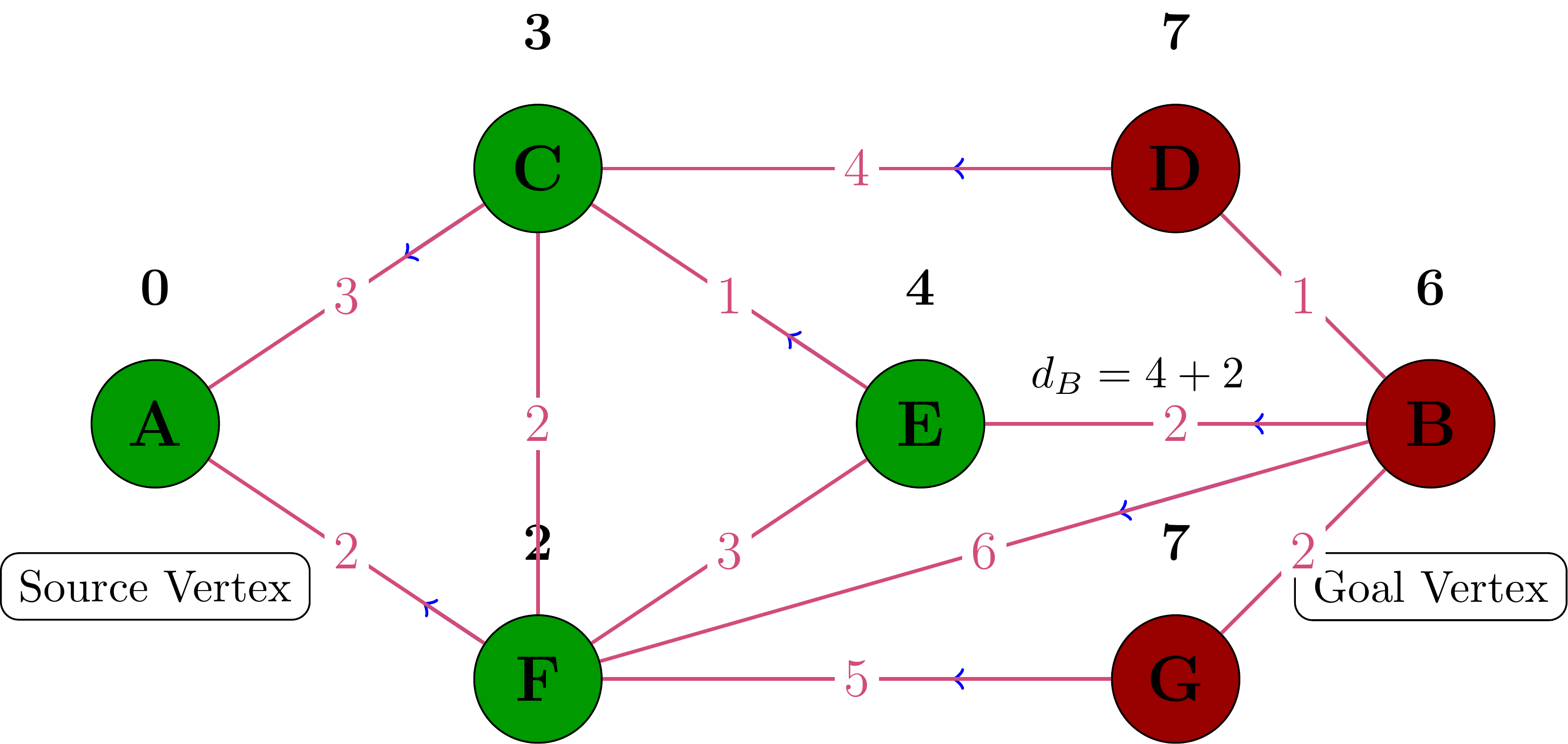
Processing Vertex B

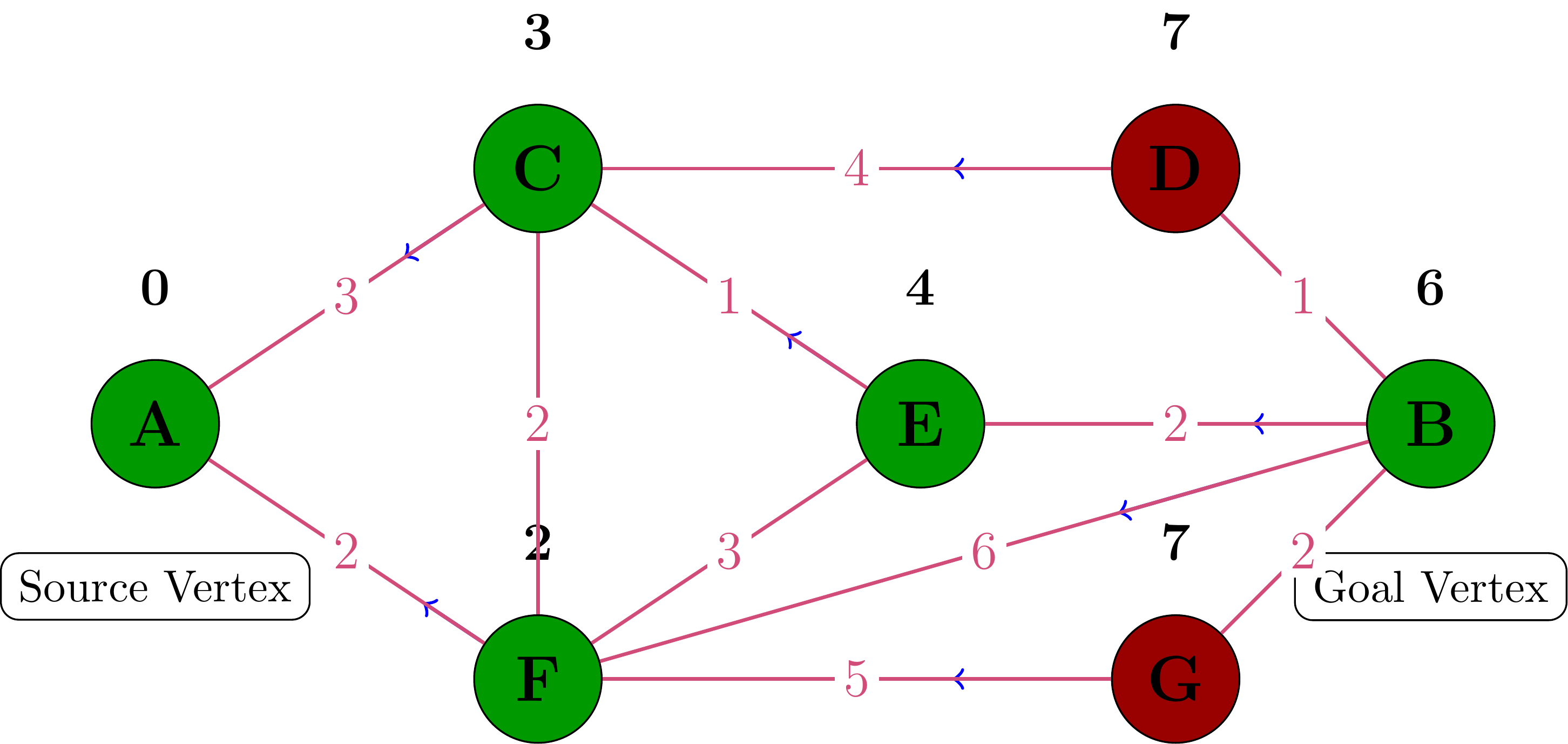
Shortest Path from B to A

Python Implementation

A full Python implementation of Dijkstra’s algorithm is available in my repository:
algorithms/classical/dijkstra.py

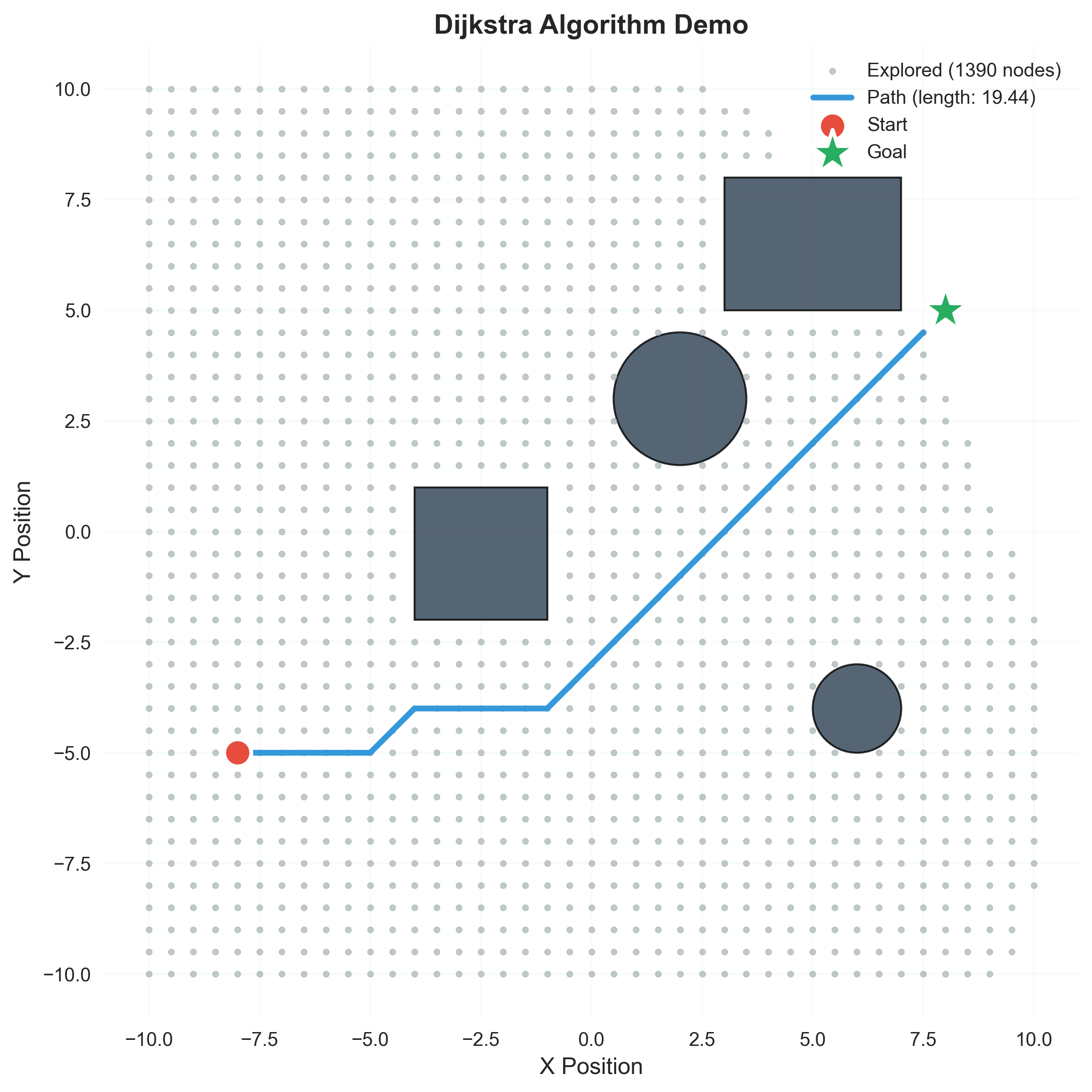
Example Output

Below are example outputs of Dijkstra’s algorithm visualized on a grid. The image demonstrates the algorithm navigating around obstacles.