Robot Arm 2D Forward / Inverse Kinematics
Published:
Overview
Both Forward Kinematics (FK) and Inverse Kinematics (IK) will be computed and simulated for the following scenarios in 2D.
- Single Joint Robot Arm
- Two-joint Robot Arm
- Multi-joint Robot Arm
Forward Kinematics: Where will the system be located at, given I rotate my arm by some known quantity?
Inverse Kinematics: How should I rotate my arm so that my system ends up at some specified location?
View Code Repository: Robot Arm Repository
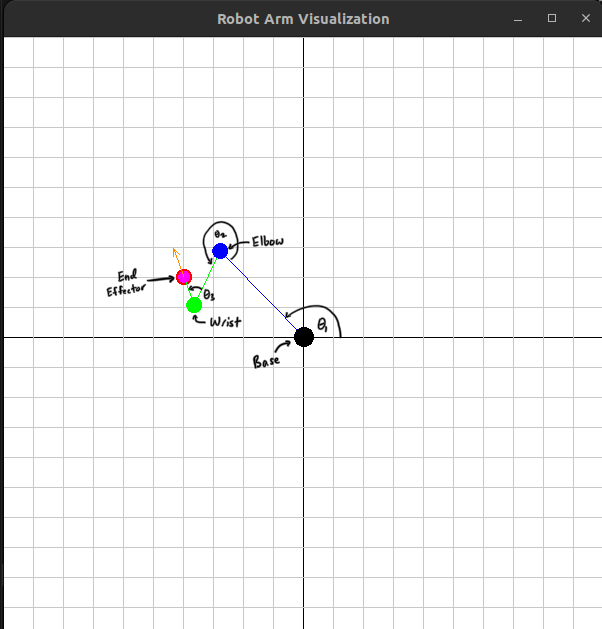
Triple Joint Robot Arm
The triple joint robot arm is especially interesting:
- A third joint (wrist) is introduced
- Providing only an \((x,y)\) target will no longer be sufficient to fully constrain the output
- The target is adjusted to \((x, y, \phi)\)
Forward Kinematics
Equations
Elbow Position:
- \[\theta _{elbow} = \theta _1\]
- \[elbow_x = L_1 * cos(\theta _{elbow})\]
- \[elbow_y = L_1 * sin(\theta _{elbow})\]
Wrist Position:
- \[\theta _{wrist} = \theta _{elbow} + \theta _2\]
- \[wrist_x = elbow_x + L_2 * cos(\theta _{wrist})\]
- \[wrist_y = elbow_y + L_2 * sin(\theta _{wrist})\]
End Effector Position / Orientation:
- \[\theta _{effector} = \theta _{wrist} + \theta _3\]
- \[end_x = wrist_x + L_2 * cos(\theta _{effector})\]
- \[end_y = wrist_y + L_2 * sin(\theta _{effector})\]
Inverse Kinematics
Intuitively, we want to use our target \(\phi\) and \(L_3\) to figure out where the wrist needs to be. Then we use the wrist position as our \((x,y)\) target and run the same logic as the double joint.
Equations
Calculate where the wrist position should be:
- \[x_{wrist} = x_{target} - L_3 * cos(\phi)\]
- \[y_{wrist} = y_{target} - L_3 * sin(\phi)\]
Define \(\theta _3\) as relative to the current orientation but derived from phi
- \[\theta _3 = \phi - \theta _1 - \theta _2\]
Use \((x_{wrist}, y_{wrist})\) instead of \((x,y)\) and copy the Double Joint Robot Inverse Kinematics Solution.
Double Joint IK Solution
Given a target position \((x_{wrist},y_{wrist})\):
\[\theta_2 = \arccos\left(\frac{d^2 - L_1^2 - L_2^2}{2L_1L_2}\right)\] \[\theta_1 = \text{atan2}(y_{wrist},x_{wrist}) - \text{atan2}(k_2, k_1)\]where:
\[k_1 = L_1 + L_2\cos(\theta_2)\] \[k_2 = L_2\sin(\theta_2)\] \[d = \sqrt{x_{wrist}^2 + y_{wrist}^2}\]Double Joint Robot Arm
Two joints are defined, where rotatation for both is along the same axis.
The Forward Kinematics are super straightforward, though the Inverse Kinematics become more complicated.
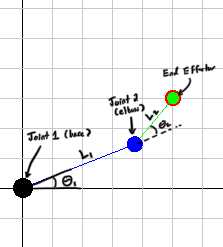
Forward Kinematics
Equations
Elbow Position:
- \[elbow_x = L_1 * cos(\theta _1)\]
- \[elbow_y = L_1 * sin(\theta _1)\]
End Effector Position:
- \[end_x = elbow_x + L_2 * cos(\theta _1 + \theta _2)\]
- \[end_y = elbow_y + L_2 * sin(\theta _1 + \theta _2)\]
Inverse Kinematics
The problem setup is defined in order to solve the inverse kinematics.
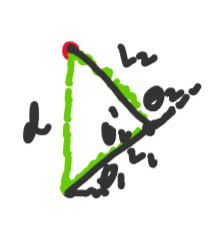
Derivation
Calculate the straight line distance from the base joint \((0,0)\) to the target \((x,y)\):
\[d = \sqrt{x^2 + y^2}\]Recall the law of cosines:
\[c^2 = a^2 + b^2 - 2ab\cos(C)\] \[d^2 = L_1^2 + L_2^2 + 2L_1L_2\cos(\theta_2)\]Solve for \(\theta_2\):
\[2L_1L_2\cos(\theta_2) = d^2 - L_1^2 - L_2^2\] \[\cos(\theta_2) = \frac{d^2 - L_1^2 - L_2^2}{2L_1L_2}\] \[\theta_2 = \arccos\left(\frac{d^2 - L_1^2 - L_2^2}{2L_1L_2}\right)\]Now solve for \(\theta_1\). Start with the forward kinematics:
\[x = L_1\cos(\theta_1) + L_2\cos(\theta_1+\theta_2)\] \[y = L_1\sin(\theta_1) + L_2\sin(\theta_1 + \theta_2)\]Expand using angle addition formulas:
\[x = L_1\cos(\theta_1) + L_2(\cos(\theta_1)\cos(\theta_2) - \sin(\theta_1)\sin(\theta_2))\] \[y = L_1\sin(\theta_1) + L_2(\sin(\theta_1)\cos(\theta_2) + \cos(\theta_1)\sin(\theta_2))\]Group by \(\cos(\theta_1)\) and \(\sin(\theta_1)\):
\[x = \cos(\theta_1)[L_1 + L_2\cos(\theta_2)] - \sin(\theta_1)[L_2\sin(\theta_2)]\] \[y = \sin(\theta_1)[L_1 + L_2\cos(\theta_2)] + \cos(\theta_1)[L_2\sin(\theta_2)]\]Define constants \(k_1\), \(k_2\) to simplify the expression since \(\theta_2\) is known:
\[k_1 = L_1 + L_2\cos(\theta_2)\] \[k_2 = L_2\sin(\theta_2)\]So,
\[x = k_1\cos(\theta_1) - k_2\sin(\theta_1)\] \[y = k_1\sin(\theta_1) + k_2\cos(\theta_1)\]We have two equations, two unknowns.
Find \(\cos(\theta_1)\) by multiplying both equations by constants: \(k_1 \cdot x\), \(k_2 \cdot y\):
\[k_1x = k_1^2\cos(\theta_1) - k_1k_2\sin(\theta_1)\] \[k_2y = k_1k_2\sin(\theta_1) + k_2^2\cos(\theta_1)\]Adding the equations gives:
\[\cos(\theta_1) = \frac{k_1x + k_2y}{k_1^2 + k_2^2}\]Subtracting the first equation from the second gives:
\[\sin(\theta_1) = \frac{k_1y - k_2x}{k_1^2 + k_2^2}\]Now we can solve for \(\theta_1\) directly:
\[\theta_1 = \text{atan2}(\sin(\theta_1), \cos(\theta_1))\] \[\theta_1 = \text{atan2}\left(\frac{k_1y - k_2x}{k_1^2 + k_2^2}, \frac{k_1x + k_2y}{k_1^2 + k_2^2}\right)\]Simplifying (common denominator cancels):
\[\theta_1 = \text{atan2}(k_1y - k_2x, k_1x + k_2y)\]By properties of atan2:
\[\theta_1 = \text{atan2}(y,x) - \text{atan2}(k_2, k_1)\]Final Solution
Given a target position \((x,y)\):
\[\theta_2 = \arccos\left(\frac{d^2 - L_1^2 - L_2^2}{2L_1L_2}\right)\] \[\theta_1 = \text{atan2}(y,x) - \text{atan2}(k_2, k_1)\]where:
\[k_1 = L_1 + L_2\cos(\theta_2)\] \[k_2 = L_2\sin(\theta_2)\] \[d = \sqrt{x^2 + y^2}\]Code
Double Joint Robot Simulation Code
Single Joint Robot Arm
A single joint is defined, where rotation along one axis is defined.
All movement is governed by a PID controller.
Forward Kinematics
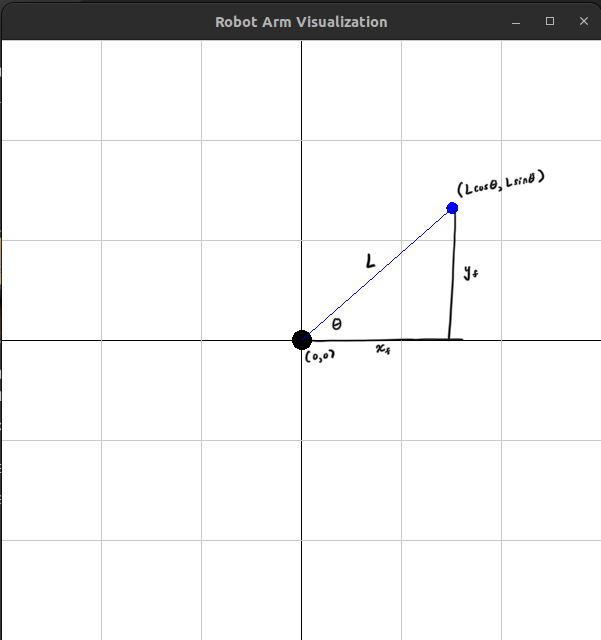
Equations
Solve for \(x_f\) and \(y_f\)
- \[x_f = L \cos(\theta)\]
- \[y_f = L \sin(\theta)\]
Toy Example
- L = 3
- \(\theta\) = 60 deg
- \(x_f = Lcos(\theta)\) = 3 * cos(60) = 1.5
- \(y_f = Lsin(\theta)\) = 3 * sin(60) = 2.598
Inverse Kinematics
Code
Single Joint Robot Simulation Code
Equations
Solve for \(\theta\)
- \[\theta = arctan(y_f/x_f)\]
Toy Example
- L = 3
- \((x_f, y_f)\) = (1.5, 2.598)
- \(tan(\theta) = y/x\) _
- \(\theta = arctan(y/x) = arctan(2.598/1.5)\) _
- \(\theta\) = 60 deg
This can be gut-checked against our FK calculations.
